 |
Composed of 30 degree/60-degree/90-degree triangles, this new hexaflexagon displays some groundbreaking characteristics. It flexes into a non-hexagonal shape and mixes triangles from its six basic faces to form hybrid faces.
by Ann Schwartz
Introduction
I first fell in love with flexagons back in 1966. My older sister Martha had either came across Martin Gardner’s Scientific American article on hexaflexagons or borrowed one of his Mathematical Puzzles and Diversions books from the library. The two of us—she a college student home for summer, and I, a 17-year-old high school student—were soon making and elaborately decorating piles of hexa-hexa-flexagons. During this time I rediscovered the Flexagon Committee's 12- and 24-faced flexagons, made a flexing triangle, and folded what I thought was a tri-tetra-flexagon, a square composed of 8 right triangles. It was several decades later, when exploring flexagons on the Internet, that I found out that my square had actually four faces, and that very few flexamaniacs seemed to know about this wonderful flexagon. I wondered if my flexing triangle was a known quantity or not, and looked, unsuccessfully, for the original model through piles of memorabilia. While trying to recreate it, I hit upon this 12-gon.
THE HEXA-DODECA-FLEXAGON
This hexagonal flexagon, which I also refer to as a 12-gon, is composed of twelve 30-degree/60-degree/90-degree right triangles and has six basic faces. It is an advanced flexagon, and flexamaniacs should be familiar with the hexahexaflexagon, and if possible, the triangle-composed square flexagon, also known as the 8-gon, or tetra-octa-flexagon, which is thoroughly described in Build Your Own Polyhedra, by Peter Hilton and Jean Pedersen (Pearson Learning). You’ll need to be able to do what Hilton and Pedersen call the "pass-through" and "reverse pass-through" flexes in order to flex in what I call Mode 2. But Mode 1 is much more fun and requires only the "pinch" a.k.a., the "straight" flex that you do when you flex a hexaflexagon. So if you’ve made hexaflexagons, I urge you to give the 12-gon a try.
Traces in the Literature
Anthony S. Conrad’s paper, "The Theory of the Flexagons," has diagrams for 2 fascinating flexagons (see "More Flexagons" and Figure 29, page 20). One is identical to one of the patterns produced when you fold up the 12-gon (see Figure 13 in this article). Flexagons Inside Out by Les Pook (Cambridge University Press) also contains "nets," or blueprints for flexagons, made of right triangles.
General Characteristics
The hexa-dodeca is deliciously similar to the hexaflexagon and 8-gon. Like the earlier flexagons, it is constructed from a straight strip of paper folded into congruent triangles. It follows the rules set forth for flexagons in general for the number of triangles needed to make it and the layers of thicknesses in 2 adjacent triangular sections. The hexa-dodeca also produces a cycle when the Tuckerman Traverse is applied to it.
Shape-Changing Flexes, Hybrid Faces, and Rogue Triangles
But the 12-gon also has some marvelous tricks of its own. Unlike its predecessors, it flexes into totally new shapes in its flattened postions. One is a hexagon in which the triangles are arranged in a nonradial fashion. The other is what can be described as a triangle-shaped propeller: a large triangle with smaller triangles arranged around it. The hexa-dodeca flexagon also naturally combines triangles from its basic faces to produce a number of hybrid faces—all this with proper flexing, no twisting or pulling. And the flexagon has what I call "rogue" triangles, a pair of triangles that swing along 1 hinge; the triangles are not attached to the flexagon on all 3 sides. Oddly enough, even when these triangles are not lying in what one would consider the right position, the hexa-dodeca still flexes smoothly.
Tips on Folding the Hexa-Dodeca
Because it is hard to manipulate 12 triangles along narrow angles without the whole flexagon turning into a jumble, I recommend making the hexa-dodeca as small as your hands will allow. I am including both formal directions following a template, and more intuitive, orgami-style directions, which I personally find much easier to use. Please note that as with all flexagons, neatness counts. Unfortunately, the diagrams in this article are homemade and sometimes the angles and line measurements are a little "off." You’ll probably have better results if you fold up the flexagon using calculator tape and not print out my diagram. I have found that making this flexagon from 2-inch wide adding machine tape and using the origami-style directions produces a flexagon that holds its shape. You may also find it helpful to paperclip the stacks of triangles together as you fold.
How to Make the 12-Gon from a Template
Fold a straight strip of paper into 37 30-degree/60-degree/90-degree triangles in the pattern in Figure 1 and number and letter the triangles as shown.
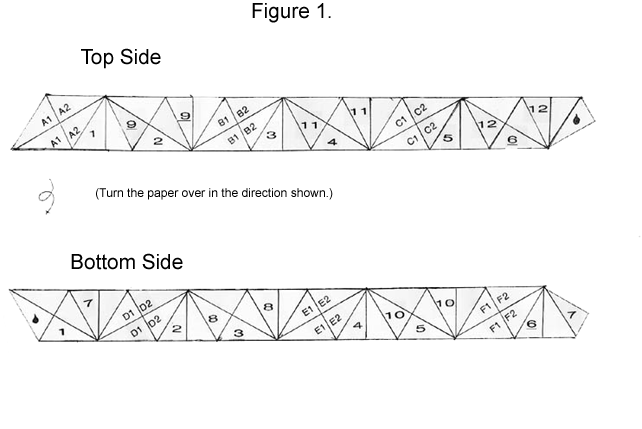 |
1. Turning the strip over and back again when you need to, fold:
triangle A1 onto
triangle A1,
triangle A2 onto triangle A2,
triangle B1 onto triangle B1,
triangle B2 onto triangle B2,
triangle C1 onto triangle C1,
triangle C2 onto triangle C2,
triangle D1 onto triangle D1,
triangle D2 onto triangle D2,
triangle E1 onto triangle E1,
triangle E2 onto triangle E2,
triangle F1 onto triangle F1,
triangle F2 onto triangle F2
…until all the lettered triangles are no longer visible, and the triangles with the droplets are lying face to face. The resulting figure is a hollow hexagon.
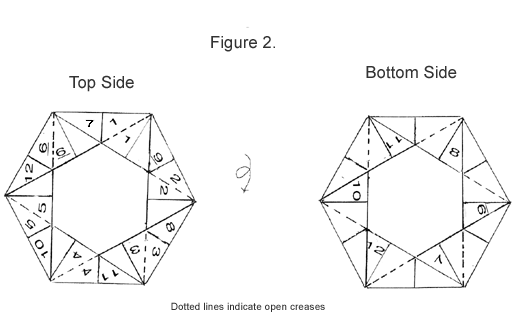 |
2. Now, flippping the strip over when you need to, fold:
triangle 1 onto triangle
1,
triangle 2 onto triangle 2,
triangle 3 onto triangle 3,
triangle 4 onto triangle 4,
triangle 5 onto triangle 5, and
triangle 6 onto triangle 6.
The strip should now look like a zig-zag.
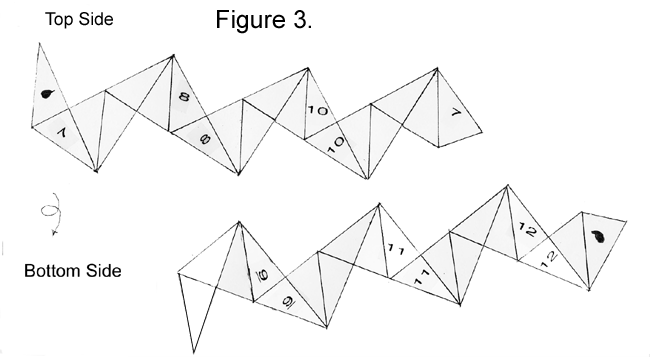 |
3. Now, again turning the strip over when you need to, fold:
triangle 8 onto triangle
8,
triangle 9 onto triangle 9,
triangle10 onto triangle 10,
triangle 11 onto triangle 11,
triangle 12 onto triangle 12
…and position triangle 7 and triangle 7 over each other.
4. Attach the triangles marked with the droplet face to face. I suggest using something like a tiny piece of tape rolled sticky side out so that the triangles can be easily detached and the flexagon unwrapped as needed. You now should have a hexagon composed of 12 triangles radially arranged.
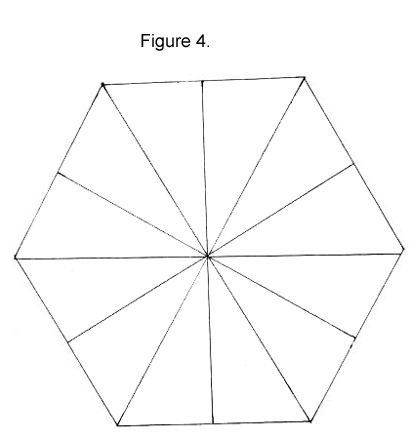 |
The triangles on the 2 visual faces of the hexagon are all blank. The numbered triangles will appear when the flexagon is flexed. The lettered triangles will always be hidden.
How to Make the 12-Gon from a Folding Pattern
With this method, the paper is folded into a tube. The interior of the tube stays hidden during flexing.
1. Take a strip of paper and create a 60-degree angle in the lower left-hand corner.
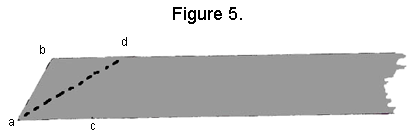 |
2. Fold down the top corner b to point c, bisecting that angle along the dotted line ad.
 |
3. Fold up, matching the edges of the paper.
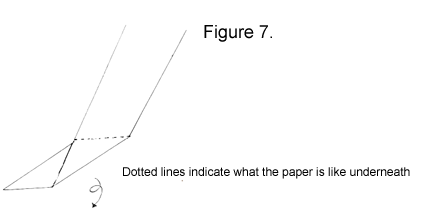 |
4. Turn the strip over and rotate it about 45 degrees.
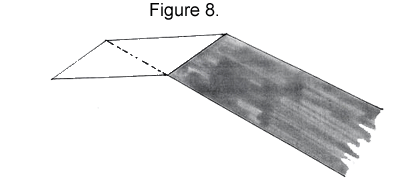 |
5. Fold up.
 |
6. Turn the strip over.
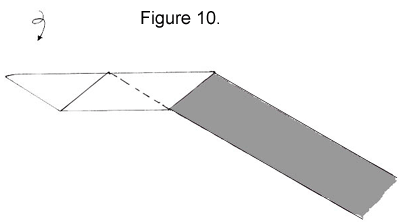 |
Copyright© Ann Schwartz 2005
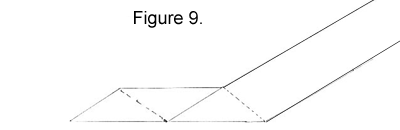
7. Fold up and notice the parallelogram shape that was formed.
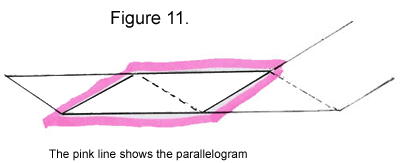 |
Copyright© Ann Schwartz 2005
8. Turn the strip over again and fold as instructed in steps 8-10, continuing to create long parallelograms. You will need 3 parallelograms, each composed of 12 30-degree/60-degree/90-degree triangles, plus 1 more triangle after the last parallelogram. That will give you the 37 triangles per side needed. I find it easier to create more triangles than necessary and then unwrap the strip and trim it later.
9. Now, position the strip the way it is pictured in Figure 12.
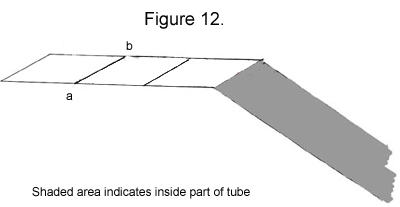 |
10. Fold up along ab.
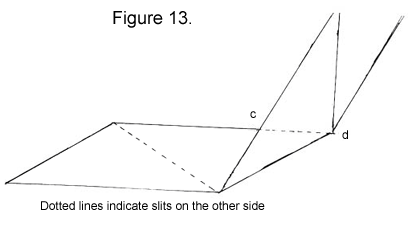 |
Copyright© Ann Schwartz 2005
11. Make a convex fold (a "mountain" fold, in origami terms) along cd.
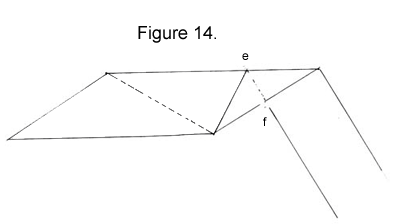 |
12. Make a mountain fold along ef. You’ve just formed the first of the 12 triangles that will make up the hexagon.
|
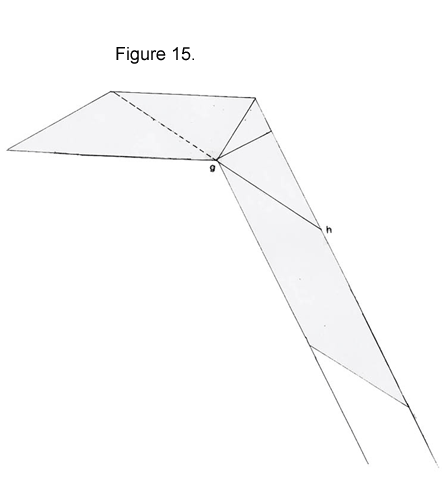
13. Fold up long line gh
…and then, starting at the next open crease, repeat steps 10-13, until your have created all the 12 triangles and have formed a whole hexagon.
13. If you haven’t counted out 37 triangles for each side, press down on all folds as hard as you can and partially unwrap the flexagon. Using the pattern of triangles in Figure 1 if you need to, make sure your strip, when folded around itself and showing the parallelograms, has 37 triangles on each side. Following Figure 1, mark the 2 triangles that will be glued together. Trim the strip if you need to, and fold it again into the hexagon. Attach the "droplet" triangles together face to face to close the flexagon. Again, I suggest using something like a tiny piece of tape rolled sticky side out that can be easily detached. The flexagon should now look like Figure 4. This is Position 1 of the 12-gon.
Flexing the Hexa-Dodeca-Flexagon
Because the flexagon has twelve creases, it can be flexed in 2 basic ways. The most fascinating is flexing along 3 creases. Unfortunately, you must flex carefully, and I know this can be difficult and frustrating with the 12-gon’s narrow angles. It’s easy to twist this flexagon’s triangles out of order so it is no longer folded and flexing properly.
Tip: No matter what method you use to fold up the 12-gon, I suggest you unfold you flexagon and add colored dots to the triangles so you can best observe this flexagon’s characteristics in action.
 |
Mode 1: Flexing Along 3 Creases
To flex along 3 creases, you only need to know the pinch flex, sometimes called the straight flex, that is used for the hexahexaflexagon.
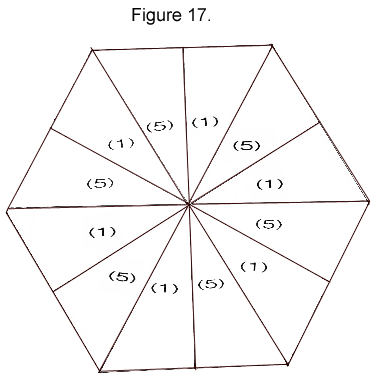
Position 1
After assembly, the flexagon’s triangles are radially arranged in alternating groups of thicknesses, the layers of paper heaped up in the individual piles of triangles. These layers are indicated by the numbers in the parentheses.
 |
Copyright© Ann Schwartz 2005
Following the rules of flexagons, the number of thicknesses of 2 adjacent triangles adds up to the total number of faces. Now we can see that the 12-gon conclusively has 6 faces. In the case of this flexagon, however, we’ll have to call them basic faces, because it mixes triangles from different basic faces to form mixed faces.
With the hexa-dodeca in Postion 1, flex along 3 equidistant creases from the corners of the hexagon.
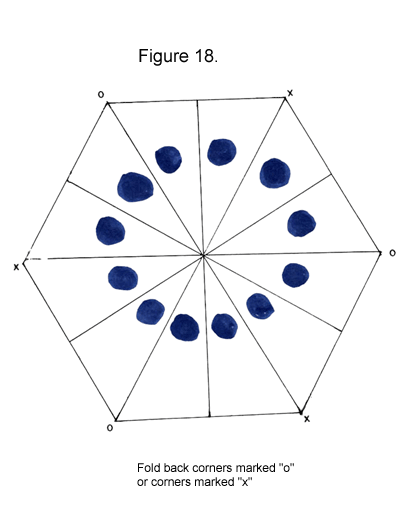 |
Position 2
This first flex will produce either Position 2 or Position 4. For argument’s sake, let’s assume it’s Position 2, a hexagon with triangles arranged in different pattern from Figure 1.
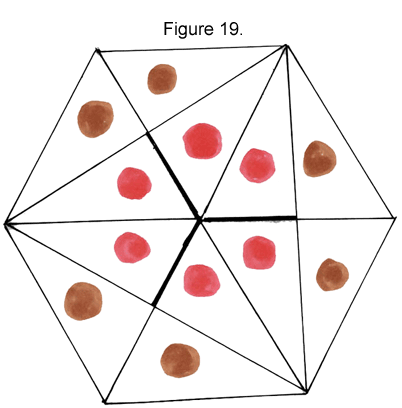 |
Position 2 can have triangles from 1 face, or it can be a hybrid face with the 6 outermost triangles from 1 face, and the inner 6 triangles, which form their own large triangular pattern, from another. Note the pattern of the thicknesses in Position 2.
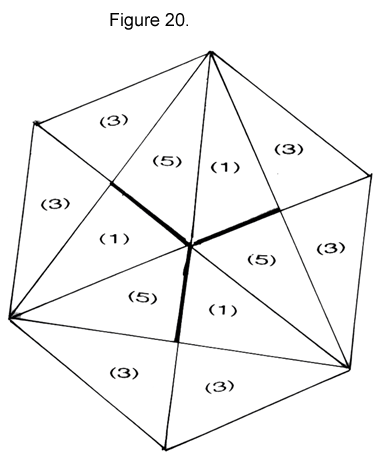 |
Rogue Triangles
This position sometimes brings up 2 "rogue" triangles, 2 outermost triangles that are not attached by folds to 1 of the their adjacent triangles. Just keep these triangles lying in position so that the flexagon retains its hexagonal shape and you should be fine. It’s interesting to note that even when these "loose-on-one-corner" triangles are folded over in a "wrong" position, the flexagon still flexes smoothly and the flexer can refold the open triangles when they reappear without unwrapping the flexagon.
Position 3
From Position 2, the 12-gon can be flexed 2 different ways. One is along its most open axes: ab, ac, and ae shown in Figure 21.
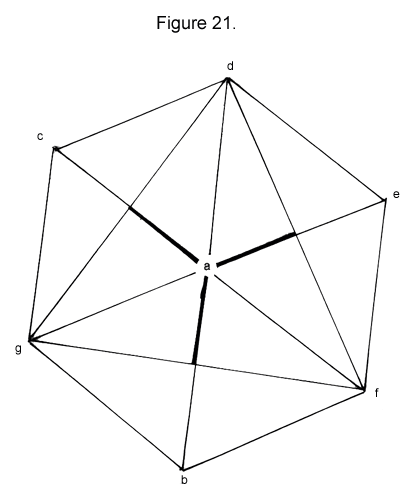 |
Note that these pathways are half crease, half open space. Now fold back corners d, f, and g to execute a pinch flex. It will bring you to something that looks like Position 1. However, now the layers of triangles are arranged differently.
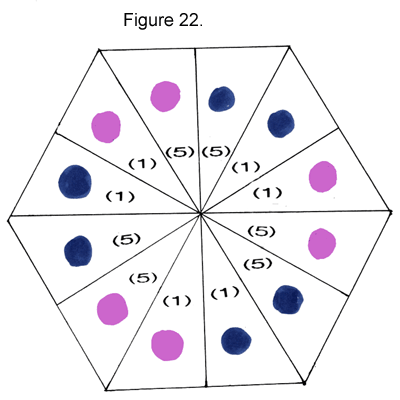 |
Position 4
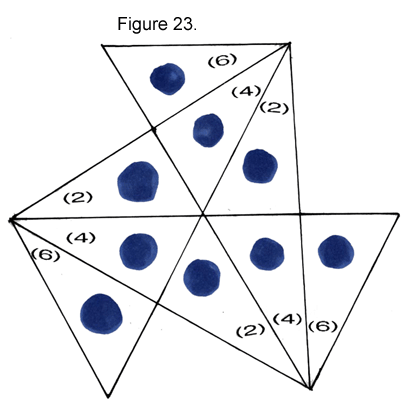
From Position 3 (radial variant), you can flex along one set of axes only. It will bring you to Position 4, the most bizarre face of all, the triangle-shaped propeller…or should it be called a propeller-shaped triangle?
 |
Copyright© Ann Schwartz 2005
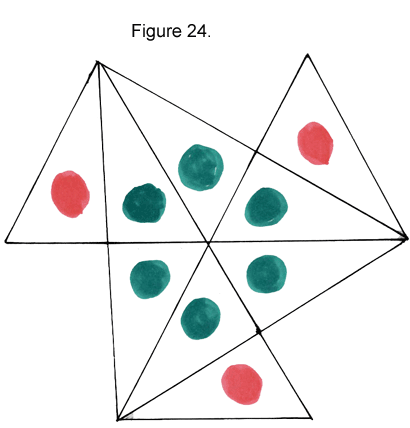
Now, things are even more interesting. Whoever thought a flexagon could morph into something so radically different looking in its flattened state? Again, the piles of triangles are arranged in combinations that equal or add up to six. Rogue triangles can appear in Position 4 as well as in Postion 2. And sometimes the 12-gon in Position 4 will display triangles that are all from 1 face; more will have triangles from 2 different faces, in other words, hybrid faces.
 |
Notes on the Faces
Keep flexing until you can bring up all 6 versions of the propeller. Like the hexaflexagon and the 8-gon, the 12-gon produces different design patterns on its flip side, so be sure to turn the flexagon over. You’ll need to do this to see all the version of the propeller. Note that the 12-gon has dominant and subdominant faces: some faces have all 12 triangles needed for a face while others only have 6, and must combine with triangles from a dominant face to form a complete hexagon or propeller.
Position Variations
One more plot wrinkle: Variations of Positions 2 and 4 will appear if the rogue triangles are folded over. For instance, the propeller in Figure 25 has a pair of rogue triangles, A and B. They are lying in the "correct" position in the drawing on the left. In the drawing on the right, they have swung to the right on hinge cd, exposing triangles from other faces. Note the change of thicknesses. The bottom picture shows the flexagon in Position 2 with a missing triangle due to rogue triangles.
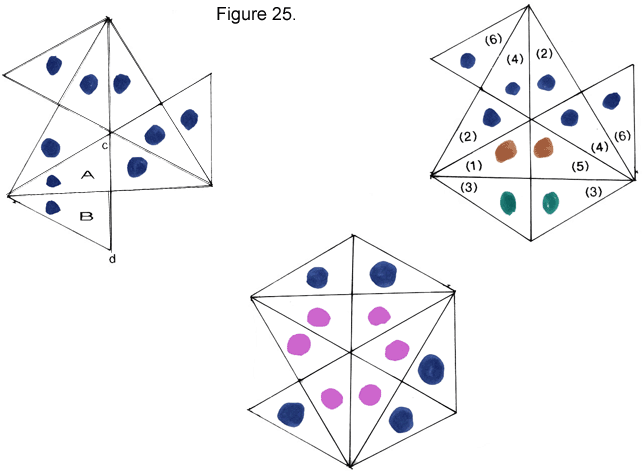 |
Just keep flexing, missing triangles and all. The 12-gon can sort itself out.
Mode 2: Flexing Along 6 Creases
As far as I know, the hexa-dodeca can be flexed along 6 equidistant creases in 2 different ways, and only from Position 1. The first is by doing a longer version of the pass-through-flex described in Build Your Own Polyhedra. This somersault of a flex basically turns the flexagon inside-out. You end up right back where you started.
A Very Complex Flex
But what happens if we were to interrupt this flex halfway and execute a version of Hilton and Pedersen’s reverse pass-through flex? This produces a hybrid face with alternating pairs of triangles from 2 different faces. Executing a pass-through-flex at this point, simply returns you to this mixed face. Execute a reverse pass-through flex to return the triangles to the starting position after folding. It may be easier to unwrap and refold your flexagon, matching color dot to color dot and blank triangles to blank triangles. (That’s what I just did!) This is as far as I have gone with the 6-crease flex. I invite you to discover any more secrets lurking in its folds!
And for Extra Credit…
To uncover a repeating cycles that exposes all the faces in all their variations—in other words, do the Tuckerman Traverse—flex the 12-gon along 1 corner in Mode 1 as often as possible, moving over 1 crease in the same direction when you must. If you’re feeling really ambitious, make the 12-gon with twice the number of faces. It can be done, and I can attest that you will produce 2 sets of rogue triangles that lie on top of each other.
Conclusion
I hope you stick with this marvelous, difficult flexagon and enjoy this brave new world of "flexagination" as much as I do. Please feel free to e-mail any comments or discoveries you make to me. For instance, flexaginator Phil Mitchell points out that the lettered triangles can be glued together; they do not contribute to the flexing of the hexagon.
I’ve also been discovering a family of pinwheel shaped flexagons—maybe they should be called flexaforms, since they are not regular polygons. One is a circular pinwheel with 16 pats and 10 faces—either a dream or a nightmare, depending on your point of view. Another is a 4-faced square with 4 protruding triangles. All are made of straight strips and use noncongruent triangles. I’ll be posting directions for them soon. And whatever your level of flexagination, keep flexing!
Ann Schwartz heads the cover copy department at a major book publisher. When not banging her head against the wall trying to dream up yet another story line for a paperback thriller or romance, she makes jewelry and folds paper into tiny triangles. She lives in Manhattan with her husband and welcomes e-mail on flexagons at annschwartz101@aol.com. She thanks all her Internet flexagon friends for their help, especially Vern Gutenkunst (http://www.trailblazingflexagons.com) for his constant encouragement, support, and research.
Copyright© 2005 Ann Schwartz EighthSquare.com P.O. Box 580 New York, NY 10113

